algo.SSpaths

The algo.SSpaths procedure returns all shortest paths from a source node to multiple reachable nodes, subject to constraints like cost, path length, and number of paths to return.

Syntax

CALL algo.SSpaths({
  sourceNode: <node>,
  relTypes: [<relationship_type>],
  weightProp: <property>,         // optional
  costProp: <property>,           // optional
  maxCost: <int>,                 // optional
  maxLen: <int>,                  // optional
  relDirection: "outgoing",      // or "incoming", "both"
  pathCount: <int>
})
YIELD path, pathWeight, pathCost

Parameters

Name	Type	Description
sourceNode	Node	Starting node
relTypes	Array	List of relationship types to follow
weightProp	String	Property to minimize along the path (e.g., dist, time)
costProp	String	Property to constrain the total value (optional)
maxCost	Integer	Upper bound on total cost (optional)
maxLen	Integer	Max number of relationships in the path (optional)
relDirection	String	Traversal direction (outgoing, incoming, both)
pathCount	Integer	Number of paths to return (0 = all shortest, 1 = default, n = max number of results)

Returns

Name	Type	Description
path	Path	Discovered path from source to target
pathWeight	Integer	Sum of the weightProp across the path
pathCost	Integer	Sum of the costProp across the path (if used)

Examples:

Lets take this Road Network Graph as an example:

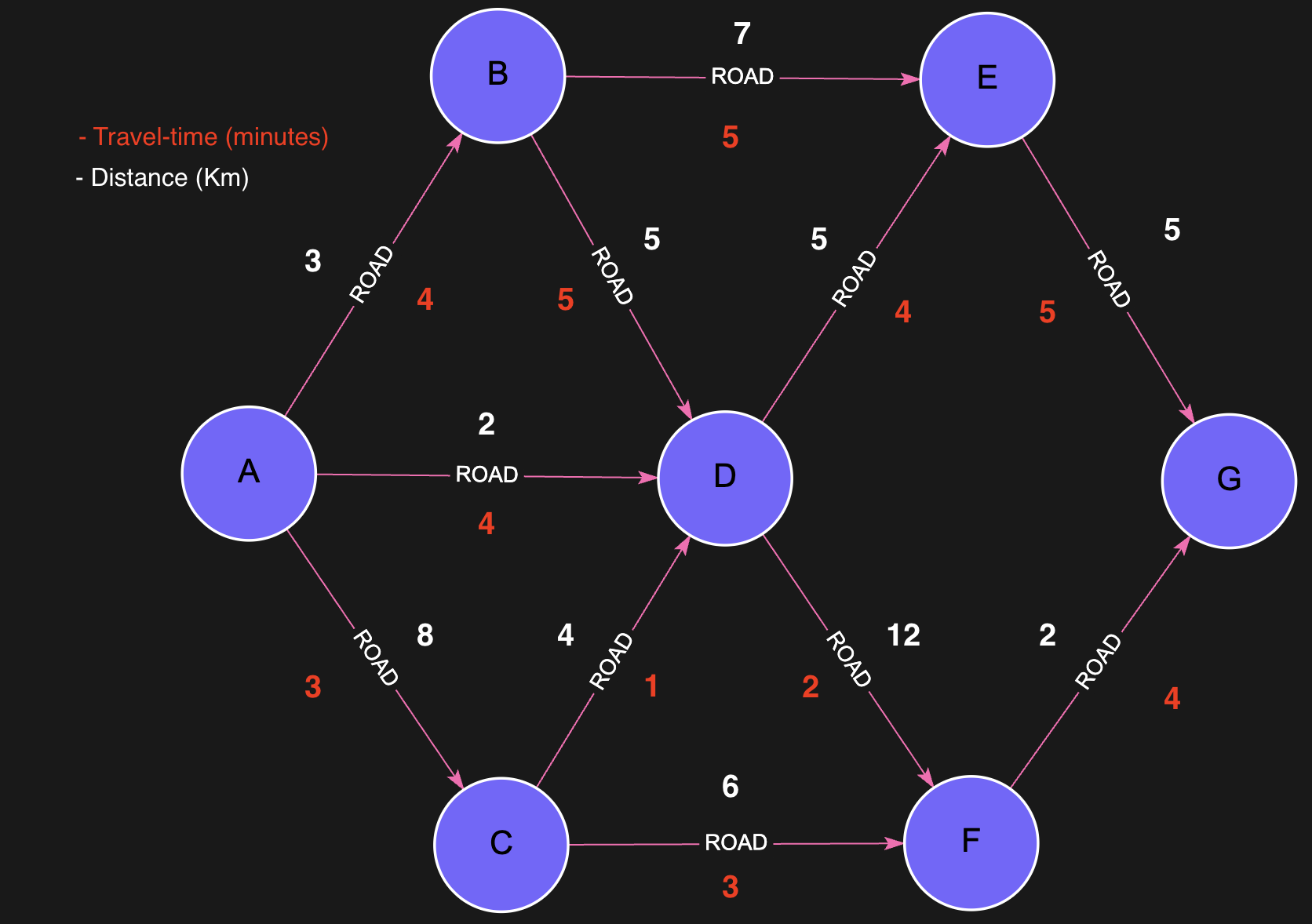
Example: All Shortest Paths by Distance (up to 10 km)

MATCH (a:City{name:'A'})
CALL algo.SSpaths({
  sourceNode: a,
  relTypes: ['Road'],
  costProp: 'dist',
  maxCost: 10,
  pathCount: 1000
})
YIELD path, pathCost
RETURN pathCost, [n in nodes(path) | n.name] AS pathNodes
ORDER BY pathCost

Expected Result:

pathCost	pathNodes
2	[A, D]
3	[A, B]
6	[A, D, C]
7	[A, D, E]
8	[A, B, D]
8	[A, C]
10	[A, B, E]

---

Example: Top 5 Shortest Paths from A by Distance

MATCH (a:City{name:'A'})
CALL algo.SSpaths({
  sourceNode: a,
  relTypes: ['Road'],
  weightProp: 'dist',
  pathCount: 5
})
YIELD path, pathWeight, pathCost
RETURN pathWeight, pathCost, [n in nodes(path) | n.name] AS pathNodes
ORDER BY pathWeight

Expected Result:

pathWeight	pathCost	pathNodes
2	1	[A, D]
3	1	[A, B]
6	2	[A, D, C]
7	2	[A, D, E]
8	1	[A, C]