algo.SPpaths

The algo.SPpaths procedure finds the shortest paths between a source and a target node, optionally constrained by cost, path length, and the number of paths to return.

It is designed for efficient and scalable computation of paths in large graphs, using properties like distance, time, or price as weights. For example, it can be used to find the fastest driving route between two cities, the cheapest shipping option in a logistics network, or the shortest communication path in a computer network.

Syntax

CALL algo.SPpaths({
  sourceNode: <node>,
  targetNode: <node>,
  relTypes: [<relationship_type>],
  weightProp: <property>,
  costProp: <property>,         // optional
  maxCost: <int>,               // optional
  maxLen: <int>,                // optional
  relDirection: "outgoing",    // or "incoming", "both"
  pathCount: <int>              // 0 = all, 1 = single (default), n > 1 = up to n
})
YIELD path, pathWeight, pathCost

Parameters

Name	Type	Description
sourceNode	Node	Starting node
targetNode	Node	Destination node
relTypes	Array	List of relationship types to follow
weightProp	String	Property to minimize along the path (e.g., dist, time)
costProp	String	Property to constrain the total value (optional)
maxCost	Integer	Upper bound on total cost (optional)
maxLen	Integer	Max number of relationships in the path (optional)
relDirection	String	Traversal direction (outgoing, incoming, both)
pathCount	Integer	Number of paths to return (0 = all shortest, 1 = default, n = max number of results)

Returns

Name	Type	Description
path	Path	Discovered path from source to target
pathWeight	Integer	Sum of the weightProp across the path
pathCost	Integer	Sum of the costProp across the path (if used)

Examples:

Lets take this Road Network Graph as an example:

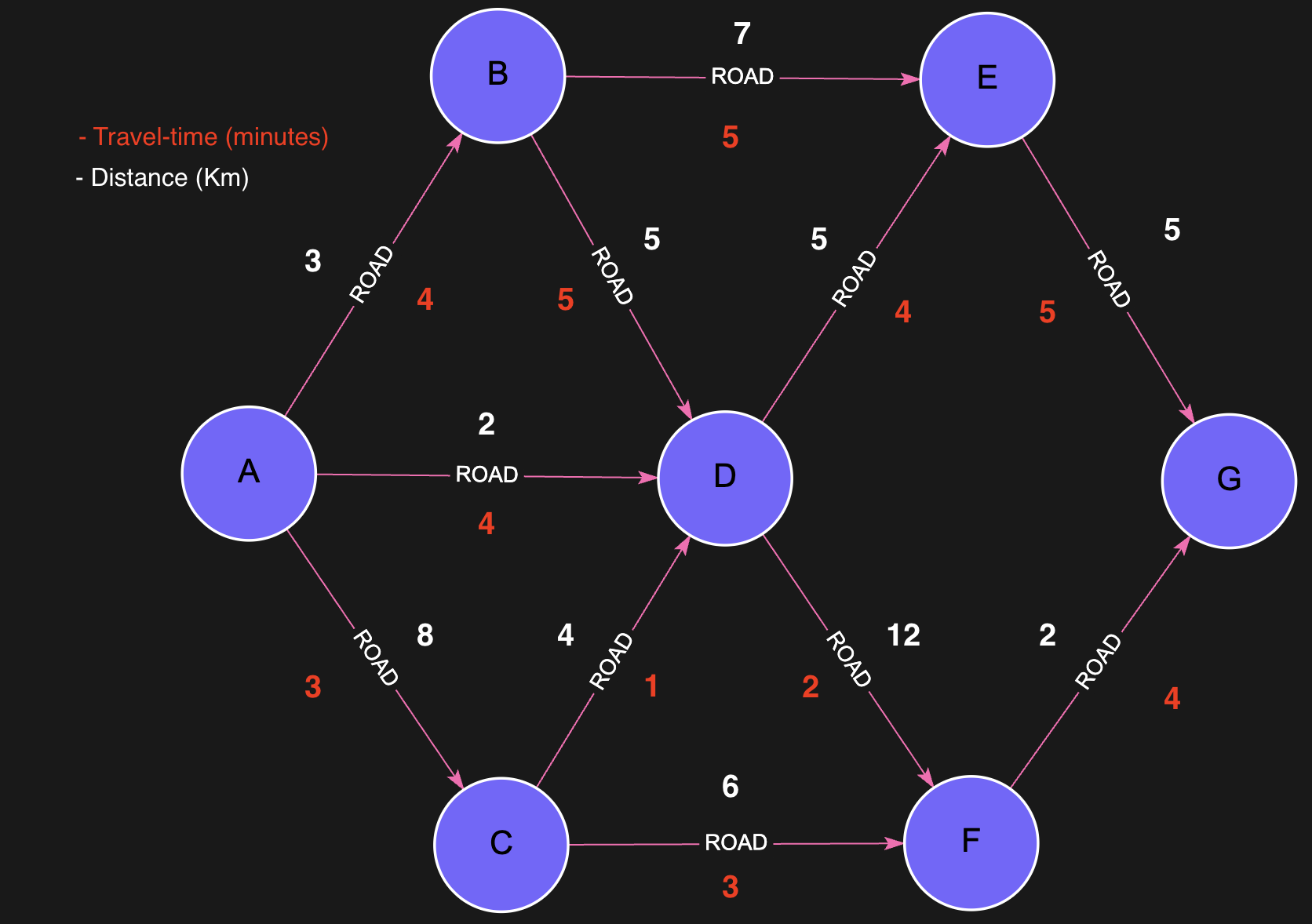
Example: Shortest Path by Distance from City A to City G:

MATCH (a:City{name:'A'}), (g:City{name:'G'})
CALL algo.SPpaths({
  sourceNode: a,
  targetNode: g,
  relTypes: ['Road'],
  weightProp: 'dist'
})
YIELD path, pathWeight
RETURN pathWeight, [n in nodes(path) | n.name] AS pathNodes

Expected Result:

pathWeight	pathNodes
12	[A, D, E G]

Example: Bounded Cost Path from City A to City G:

MATCH (a:City{name:'A'}), (g:City{name:'G'})
CALL algo.SPpaths({
  sourceNode: a,
  targetNode: g,
  relTypes: ['Road'],
  weightProp: 'dist',
  costProp: 'time',
  maxCost: 12,
  pathCount: 2
})
YIELD path, pathWeight, pathCost
RETURN pathWeight, pathCost, [n in nodes(path) | n.name] AS pathNodes

Expected Result:

pathWeight	pathCost	pathNodes
16	10	[A, D, F G]
14	12	[A, D, C F, G]

---